Siempre que tengamos que medir alguna magnitud (magnitud es todo aquello que podemos contar, medir o pesar) debemos empezar por establecer una unidad. En nuestro caso la unidad fundamental de medida de longitudes es el metro.
AMPLIANDO CONOCIMIENTOS:
- No todo son magnitudes. No podemos medir la simpatía, la belleza, la bondad….
- Cualquier unidad debe cumplir unas condiciones:
- Ha de ser constante (no puede cambiar)
- Ha de ser universal (utilizable por todos)
- Ha de ser fácil de reproducir
La unidad será siempre una cantidad arbitraria y se le asignará el valor 1.
- A lo largo del tiempo la definición de metro ha ido variando buscando una mayor exactitud.
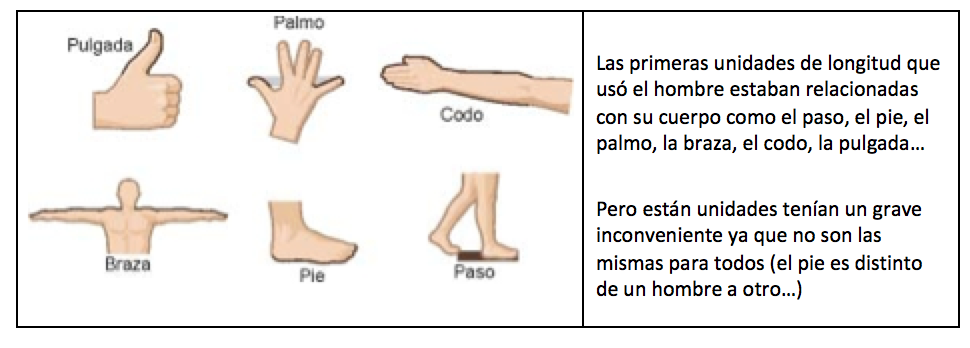
Las primeras unidades de medida fueron:
La primera definición fue dada en 1791 y la formuló la Academia de las Ciencias francesa: se define el metro como “la diezmillonésima parte del cuadrante del meridiano terrestre”.
En 1889 la Comisión Internacional de Pesos y Medidas definió el metro como “la distancia entre los extremos de una barra de platino e iridio que se conserva en el Museo de Pesos y Medidas de París”.
En 1960 se vuelve a definir al metro mediante una definición de imposible comprensión para los estudios de este curso.
La última definición es de 1983. Un metro es la distancia que recorre la luz en el vacío durante un intervalo de 1/299 792 458 de segundo. Esta definición es 1500 veces más exacta que la de 1889.
